
K-Means算法流程
step1:选择K个点作为初始质心
step2:repeat
将每个点指派到最近的质心,形成K个簇
重新计算每个簇的质心
until 质心不在变化
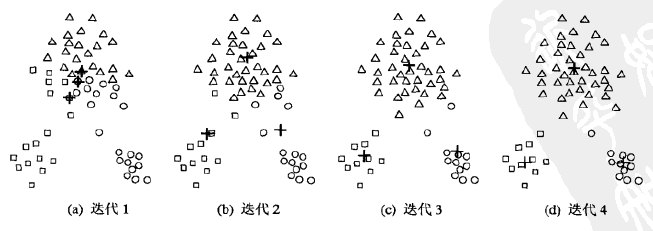
我们对每一个步骤都进行分析
step1:选择K个点作为初始质心
这一步首先要知道K的值,也就是说K是手动设置的,而不是像EM算法那样自动聚类成n个簇
其次,如何选择初始质心
最简单的方式无异于,随机选取质心了,然后多次运行,取效果最好的那个结果。这个方法,简单但不见得有效,有很大的可能是得到局部最优。
另一种复杂的方式是,随机选取一个质心,然后计算离这个质心最远的样本点,对于每个后继质心都选取已经选取过的质心的最远点。使用这种方式,可以确保质心是随机的,并且是散开的。
step2:repeat
将每个点指派到最近的质心,形成K个簇
重新计算每个簇的质心
until 质心不在变化
如何定义最近的概念,对于欧式空间中的点,可以使用欧式空间,对于文档可以用余弦相似性等等。对于给定的数据,可能适应与多种合适的邻近性度量。
其他问题
离群点的处理
离群点可能过度影响簇的发现,导致簇的最终发布会与我们的预想有较大出入,所以提前发现并剔除离群点是有必要的。
在我的工作中,是利用方差来剔除离群点,结果显示效果非常好。
簇分裂和簇合并
使用较大的K,往往会使得聚类的结果看上去更加合理,但很多情况下,我们并不想增加簇的个数。
这时可以交替采用簇分裂和簇合并。这种方式可以避开局部极小,并且能够得到具有期望个数簇的结果。
public class Point { private double x; private double y; private int id; private boolean beyond;//标识是否属于样本 public Point(int id, double x, double y) { this.id = id; this.x = x; this.y = y; this.beyond = true; } public Point(int id, double x, double y, boolean beyond) { this.id = id; this.x = x; this.y = y; this.beyond = beyond; } public double getX() { return x; } public double getY() { return y; } public int getId() { return id; } public boolean isBeyond() { return beyond; } @Override public String toString() { return "Point{" + "id=" + id + ", x=" + x + ", y=" + y + '}'; } @Override public boolean equals(Object o) { if (this == o) return true; if (o == null || getClass() != o.getClass()) return false; Point point = (Point) o; if (Double.compare(point.x, x) != 0) return false; if (Double.compare(point.y, y) != 0) return false; return true; } @Override public int hashCode() { int result; long temp; temp = x != +0.0d ? Double.doubleToLongBits(x) : 0L; result = (int) (temp ^ (temp >>> 32)); temp = y != +0.0d ? Double.doubleToLongBits(y) : 0L; result = 31 * result + (int) (temp ^ (temp >>> 32)); return result; } } Cluster.class public class Cluster { private int id;//标识 private Point center;//中心 private List members = new ArrayList ();//成员 public Cluster(int id, Point center) { this.id = id; this.center = center; } public Cluster(int id, Point center, List members) { this.id = id; this.center = center; this.members = members; } public void addPoint(Point newPoint) { if (!members.contains(newPoint)) members.add(newPoint); else throw new IllegalStateException("试图处理同一个样本数据!"); } public int getId() { return id; } public Point getCenter() { return center; } public void setCenter(Point center) { this.center = center; } public List getMembers() { return members; } @Override public String toString() { return "Cluster{" + "id=" + id + ", center=" + center + ", members=" + members + "}"; } } 抽象的距离,可以具体实现为欧式,曼式或其他距离公式 public abstract class AbstractDistance { abstract public double getDis(Point p1, Point p2); } 点对 public class Distence implements Comparable{ private Point source; private Point dest; private double dis; private AbstractDistance distance; public Distence(Point source, Point dest, AbstractDistance distance) { this.source = source; this.dest = dest; this.distance = distance; dis = distance.getDis(source, dest); } public Point getSource() { return source; } public Point getDest() { return dest; } public double getDis() { return dis; } @Override public int compareTo(Distence o) { if (o.getDis() > dis) return -1; else return 1; } }
核心实现类
public class KMeansCluster { private int k;//簇的个数 private int num = 100000;//迭代次数 private List datas;//原始样本集 private String address;//样本集路径 private List data = new ArrayList (); private AbstractDistance distance = new AbstractDistance() { @Override public double getDis(Point p1, Point p2) { //欧几里德距离 return Math.sqrt(Math.pow(p1.getX() - p2.getX(), 2) + Math.pow(p1.getY() - p2.getY(), 2)); } }; public KMeansCluster(int k, int num, String address) { this.k = k; this.num = num; this.address = address; } public KMeansCluster(int k, String address) { this.k = k; this.address = address; } public KMeansCluster(int k, List datas) { this.k = k; this.datas = datas; } public KMeansCluster(int k, int num, List datas) { this.k = k; this.num = num; this.datas = datas; } private void check() { if (k == 0) throw new IllegalArgumentException("k must be the number > 0"); if (address == null && datas == null) throw new IllegalArgumentException("program can't get real data"); } /** * 初始化数据 * * @throws java.io.FileNotFoundException */ public void init() throws FileNotFoundException { check(); //读取文件,init data //处理原始数据 for (int i = 0, j = datas.size(); i < j; i++) data.add(new Point(i, datas.get(i), 0)); } /** * 第一次随机选取中心点 * * @return */ public Set chooseCenter() { Set center = new HashSet (); Random ran = new Random(); int roll = 0; while (center.size() < k) { roll = ran.nextInt(data.size()); center.add(data.get(roll)); } return center; } /** * @param center * @return */ public List prepare(Set center) { List cluster = new ArrayList (); Iterator it = center.iterator(); int id = 0; while (it.hasNext()) { Point p = it.next(); if (p.isBeyond()) { Cluster c = new Cluster(id++, p); c.addPoint(p); cluster.add(c); } else cluster.add(new Cluster(id++, p)); } return cluster; } /** * 第一次运算,中心点为样本值 * * @param center * @param cluster * @return */ public List clustering(Set center, List cluster) { Point[] p = center.toArray(new Point[0]); TreeSet distence = new TreeSet ();//存放距离信息 Point source; Point dest; boolean flag = false; for (int i = 0, n = data.size(); i < n; i++) { distence.clear(); for (int j = 0; j < center.size(); j++) { if (center.contains(data.get(i))) break; flag = true; // 计算距离 source = data.get(i); dest = p[j]; distence.add(new Distence(source, dest, distance)); } if (flag == true) { Distence min = distence.first(); for (int m = 0, k = cluster.size(); m < k; m++) { if (cluster.get(m).getCenter().equals(min.getDest())) cluster.get(m).addPoint(min.getSource()); } } flag = false; } return cluster; } /** * 迭代运算,中心点为簇内样本均值 * * @param cluster * @return */ public List cluster(List cluster) { // double error; Set lastCenter = new HashSet (); for (int m = 0; m < num; m++) { // error = 0; Set center = new HashSet (); // 重新计算聚类中心 for (int j = 0; j < k; j++) { List ps = cluster.get(j).getMembers(); int size = ps.size(); if (size < 3) { center.add(cluster.get(j).getCenter()); continue; } // 计算距离 double x = 0.0, y = 0.0; for (int k1 = 0; k1 < size; k1++) { x += ps.get(k1).getX(); y += ps.get(k1).getY(); } //得到新的中心点 Point nc = new Point(-1, x / size, y / size, false); center.add(nc); } if (lastCenter.containsAll(center))//中心点不在变化,退出迭代 break; lastCenter = center; // 迭代运算 cluster = clustering(center, prepare(center)); // for (int nz = 0; nz < k; nz++) { // error += cluster.get(nz).getError();//计算误差 // } } return cluster; } /** * 输出聚类信息到控制台 * * @param cs */ public void out2console(List cs) { for (int i = 0; i < cs.size(); i++) { System.out.println("No." + (i + 1) + " cluster:"); Cluster c = cs.get(i); List p = c.getMembers(); for (int j = 0; j < p.size(); j++) { System.out.println("\t" + p.get(j).getX() + " "); } System.out.println(); } } } 代码还没有仔细优化,执行的效率可能还存在一定的问题